Directions (1-5): In the following questions, two equations (I) and (II) are given. You have to solve both the equations and mark the appropriate answer.
Q1. I.(x-7)²=3x-23
II. y²-21y+108=0
(a) x<y
(b) x≤y
(c) x>y
(d) x≥y
(e) x=y or no relation.
Q2. I. x³=2744
II. (y-10)²=7y-80
(a) x<y
(b) x≤y
(c) x>y
(d) x≥y
(e) x=y or no relation.
Q3. I. (x+25)²=729
II. 3y²-20y+32=0
(a) x<y
(b) x≤y
(c) x>y
(d) x≥y
(e) x=y or no relation.
Q4. I. 3x²-26x+35=0
II. 8y²-26y+21=0
(a) x<y
(b) x≤y
(c) x>y
(d) x≥y
(e) x=y or no relation.
Q5. I. 3x²-17x+10=0
II. 16y²-14y+3=0
(a) x<y
(b) x≤y
(c) x>y
(d) x≥y
(e) x=y or no relation.
Direction (6-10): Study the given passage carefully & answer the questions.
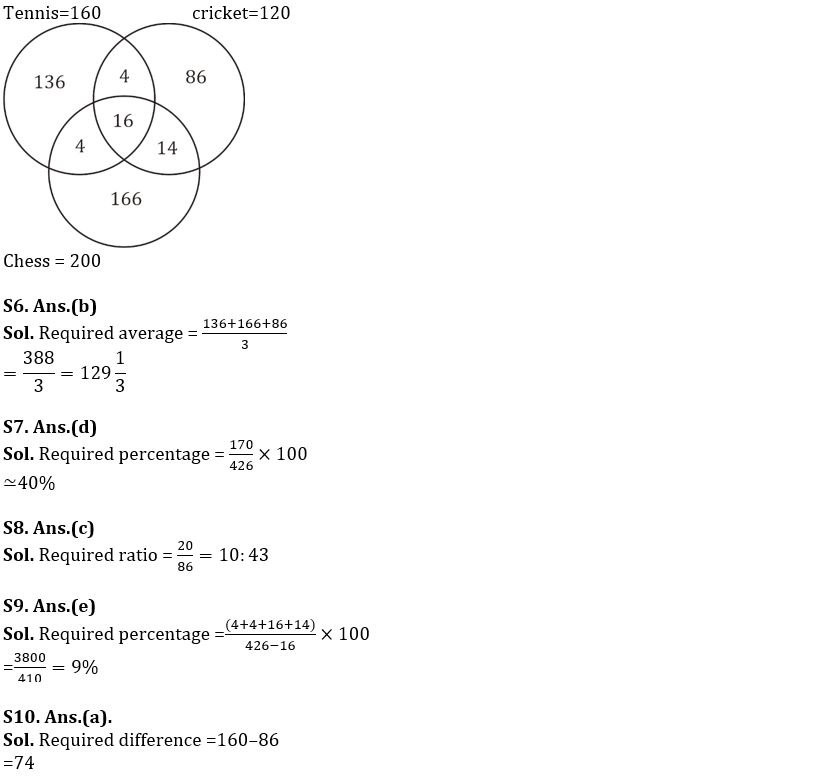
In a sport Academy ‘XY’, there are some student who can play three games i.e. tennis, cricket & chess. Total number of players who play tennis is 160 & all three games are played by 10% of total tennis players. Ratio of cricket to chess players is 3:5 and total of cricket & chess players is 100% more than tennis players. Players who play both tennis and chess are 12 ½ % of total tennis players. Ratio of players who play both tennis & cricket to players who play both chess & cricket is 2:3 & total of players who play both tennis & cricket and players who play both chess & cricket is equal to one-fourth of chess players.
Q6. What is the average no. of players who play only one game?
(a) 139⅔
(b) 129⅓
(c) 135
(d) None of these
(e) 129⅔
Q7. Players who play chess but not cricket is approximately what percent of total players?
(a) 35%
(b) 45%
(c) None of these
(d) 40%
(e) 50%
Q8. What is ratio of players who play both tennis & chess to players who play only cricket?
(a) 7 : 13
(b) 9 : 41
(c) 10 : 43
(d) None of these
(e) 2 : 5
Q9. Players who play at least two games is approximately what percent of players who play utmost two games?
(a) 4%
(b) 6%
(c) 15%
(d)12%
(e)9%
Q10. What is the difference between no. of players who can play tennis & players who play only cricket?
(a) 74
(b) 64
(c) 68
(d) None of these
(e) 72
Direction (11-15) : The given below pie chart shows the percentage distribution of daily consumption of electricity (in units) of five different families in a building. Read the pie-chart carefully and answer the following questions.
Total units of electricity consumed in a day =14,000
Note-Total units of electricity available = Total units of electricity consumed + total units of unconsumed electricity
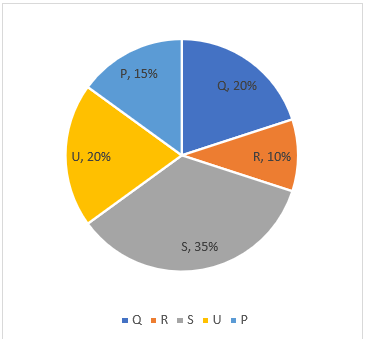
Q11. The average units of electricity consumed by families P and S together is what percent more/less than the average units of electricity consumed by families R and U together?
(a) 25%
(b) 66⅔
(c) 33⅓%
(d) 60%
(e) 75%
Q12. If 87.5% of the available units of electricity is consumed by all families, then find the ratio of units of unconsumed electricity to the difference of the units of electricity consumed by families S and Q together?
(a) 6 : 7
(b) 44 : 45
(c) 62 : 63
(d) 20 : 21
(e) 14 : 15
Q13. Find the ratio of the units of electricity consumed by family S and U together to the units of electricity consumed by families P and R together?
(a) 11 : 5
(b) 5 : 4
(c) 3 : 2
(d) 13 : 8
(e) 15 : 8
Q14. 
of units of electricity consumed by family S is what percent of units of electricity consumed by R.
(a) 7 ½ %
(b) 8 ½ %
(c) 10%
(d) 12.5%
(e) 11%
Q15. The difference of the units of electricity consumed by families U and S together is how much more than the difference of units of electricity consumed by family Q and R together?
(a) 700 units
(b) 640 units
(c) 660 units
(d) 720 units
(e) 680 units
Solutions
Quantitative Aptitude Quiz For Bank Main...
Quantitative Aptitude Quiz For Bank Foun...
