Directions (1-5): In the given questions, two quantities are given, one as ‘Quantity I’ and another as ‘Quantity II’. You have to determine relationship between two quantities and choose the appropriate option:
Q1. Quantity I: x²+16x+63=0
Quantity II: x²+25x+144=0
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or No relation
Q2. Quantity I: 3x²+22x+40=0
Quantity II: x²-16x-36=0
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or No relation
Q3. Quantity I: x²=961
Quantity II: x²-36x+155=0
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or No relation
Q4. Quantity I: x²+16x+6=72-3x
Quantity II: x²+13x-96=6+2x
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or No relation
Q5. Quantity I: x²+29x-210=0
Quantity II: x²-21x+104=0
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or No relation
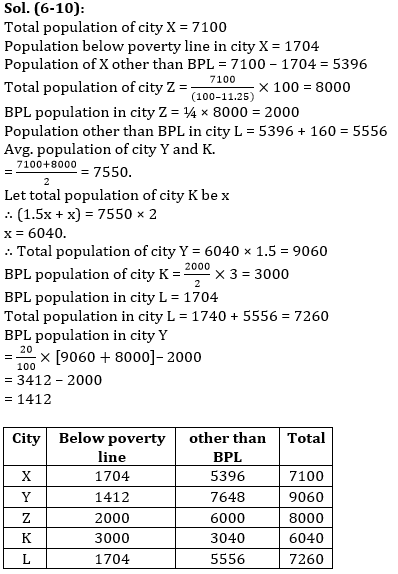
Directions (6-10): Study the given passage carefully and answer the questions.
The total population of city X is 7100 out of which 24% population are below poverty line. And total population of city X is 11 ¼ % less than total population of city Z and 25% of population in city Z is below poverty line. Population other than below poverty line in city L is 160 more than population of city X which are not below poverty line.
Average population of Y and K is equal to average population of city X and Z & population of Y is 150% of population of K. Ratio of BPL in city Z to city K is 2 : 3. 20% of total population are BPL in city Y and Z. BPL in city L is equal to BPL in city X.
Q6. Average BPL population in city X and Y is how much more/less than average BPL population in city K and L ?
(a) 794
(b) 824
(c) 848
(d) 764
(e) None of these
Q7. Average population in city K and L is what percent of total population in city Z ?
(a) 93%
(b) 73%
(c) 83.125%
(d) 87.50%
(e) 78.625%
Q8. In another city ‘A’, BPL population is half of the population other than BPL in city K which is 25% of total population. Then find total population in city A ?
(a) 6820
(b) 6080
(c) 6240
(d) None of these
(e) 6040
Q9. What is the average BPL population in all the cities ?
(a) 1924
(b) None of these
(c) 1884
(d) 1724
(e) 1964
Q10. What is the ratio of BPL population in city Y to city L ?
(a) 426 : 353
(b) 353 : 426
(c) 351 : 425
(d) None of these
(e) 353 : 428
Directions (11-15): Study the table carefully and answer the questions.
Table given below shows percentage of books sold of 3 different publications by five different seller in a month.
Note: Books are sold by three publication only.
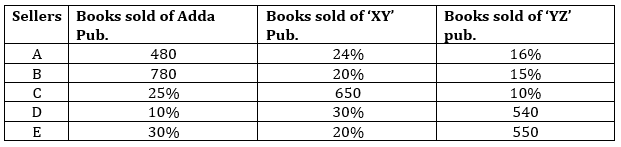
Q11. Books sold by seller B of XY and YZ pub. Together is how much more/less than books sold by E of Adda & YZ publications together ?
(a) 360
(b) None of these
(c) 380
(d) 420
(e) 460
Q12. Books sold by seller C of Adda & XY together is what percent of total books sold by seller D ?
(a) 100%
(b) 80%
(c) None of these
(d) 150%
(e) 120%
Q13. What is average number of books sold by all sellers of Adda publication ?
(a) 392
(b) 386
(c) 406
(d) None of these
(e) 414
Q14. If selling price of each book of Adda publication sold by seller C is Rs. 250 and selling price of each book of XY publication sold by seller D is Rs. 220. Then find the difference in selling price of books of Adda publication sold by C and XY publication sold by D ?
(a) Rs. 4500
(b) Rs. 2900
(c) Rs. 3600
(d) Rs. 3100
(e) Rs. 4200
Q15. If profit made on each book sold by seller E is Rs. 44. Then find profit percent of each book sold by seller E ? (given that selling price of each book is Rs. 264)
(a) 22%
(b) 25%
(c) 20%
(d) 15%
(e) 30%
Solutions
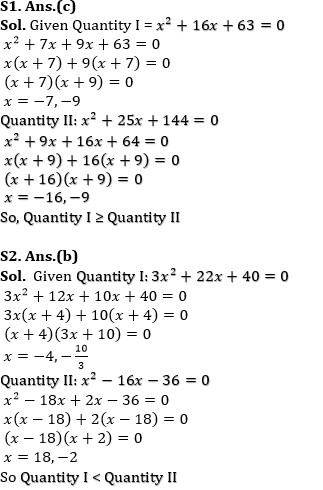

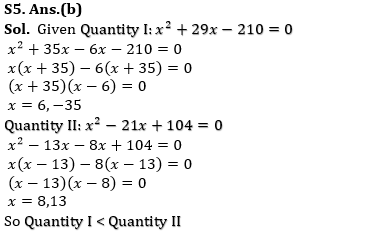


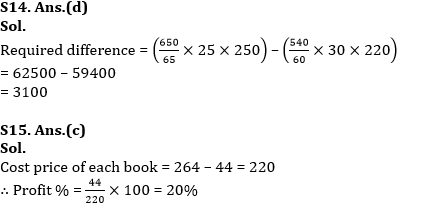











 GA Capsule for SBI Clerk Mains 2025, Dow...
GA Capsule for SBI Clerk Mains 2025, Dow...
 The Hindu Review October 2022: Download ...
The Hindu Review October 2022: Download ...
 IIFCL Assistant Manager Result 2025 Out,...
IIFCL Assistant Manager Result 2025 Out,...





