Directions (1-5): The following questions are accompanied by two statements (I) and (II). You have to determine which statements(s) is/are sufficient/necessary to answer the questions.
(a) Statement (I) alone is sufficient to answer the question but statement (II) alone is not sufficient to answer the questions.
(b) Statement (II) alone is sufficient to answer the question but statement (I) alone is not sufficient to answer the question.
(c) Both the statements taken together are necessary to answer the questions, but neither of the statements alone is sufficient to answer the question.
(d) Either statement (I) or statement (II) by itself is sufficient to answer the question.
(e) Statements (I) and (II) taken together are not sufficient to answer the question.
Q1. Ratio between length of two trains is 4 : 3. What will be difference between lengths of both trains?
I. Speed of larger trains and smaller train is 72 km/hr and 90 km/hr respectively. Both trains cross each other in 28/3 sec, when running in opposite direction.
II. Speed of smaller train is 90 km/hr and it can cross a pole in 7.2 sec.
Q2. There are three men P, Q and R. Find the difference between time taken by P & Q together to complete a task and time taken by Q & R together to complete the same task?
I. ‘R’ takes twice as much time as ‘Q’ and thrice as much time as ‘P’ takes alone.
II. If they all three works together work will be completed in 4 days.
Q3. Satish sold an article to Ayush at 20% profit. If Ayush purchased article from Satish in Rs. 1440, then find the profit percentage of Veer if Satish bought this article form Veer?
I. Veer sold the article on Rs. 240 more than its cost price to Satish.
II. If Veer sold article to Ayush on same price as Satish sold to Ayush, then he made overall profit of 50%.
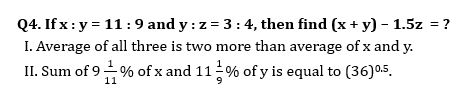
Q5. Ratio between length and breadth of rectangle ‘X’ is 7 : 4. Find area of a square ‘Y’?
I. length of rectangle ‘X’ is two times of radius of circle, whose area is 616 cm2.
II. Perimeter of rectangle ‘X’ is 20 cm more than perimeter of square ‘Y’.
Solutions
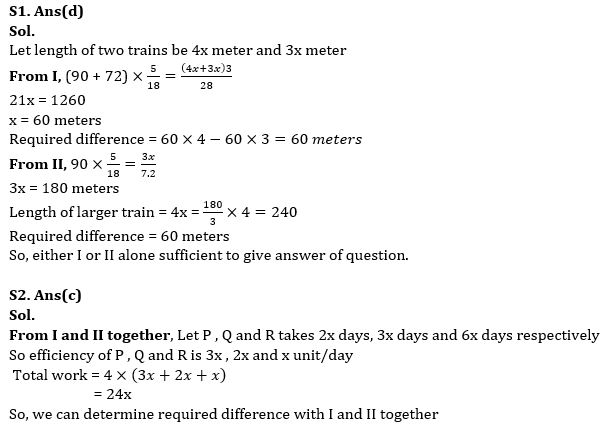



. . . .





 50+ Data Sufficiency Questions For Bank ...
50+ Data Sufficiency Questions For Bank ...
 Quantitative Aptitude Quiz For Bank Main...
Quantitative Aptitude Quiz For Bank Main...
 Quantitative Aptitude Quiz For Bank Foun...
Quantitative Aptitude Quiz For Bank Foun...





