Direction (1 -5): Given table shows the number of applications filled for three various exams (CAT, MAT & SAT) and applicants who attempted these exams in years 2018, 2019 & 2020. Read the data carefully and answer the questions. (Some data are missing which you have to calculate as per information provided in question).
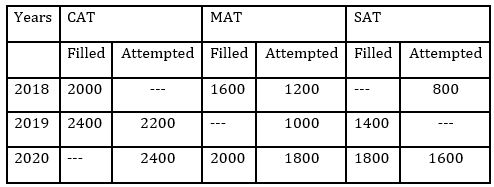
(exam & year is in format i.e. CAT 2018 is written as CAT’18)
(Each applicant filled only one form and there are only these 3 exams)
Note – Total applicants who filled the form of any exam in any year = Total applicants (who attempted + who have not attempted) that exam in that year.

Q2. Ratio of applicants who filled CAT’20 to those who attempted SAT’19 is 7 : 3 and number of applicants who attempted SAT’19 is equal to number of applicants who filled SAT’18 . If 4400 applicants filled SAT in all given years together, then find how many applicants not attempted any exam in 2020?
(a) 400
(b) 1200
(c) 800
(d) 1000
(e) 600
Q3. Average number of applicants who filled CAT in all given years is 8000/3 and percentage of applicants attempted CAT’20 out of total who filled CAT’20 is same as that for MAT’19, then in which year maximum percent of applicants attempted MAT?
(a) 2018 & 2019
(b) 2019
(c) 2019 & 2020
(d) 2018
(e) 2020
Q4. Difference between number of applicants who filled MAT and those who attempted same exam is maximum in 2018 and minimum in 2020. If number of applicants who filled MAT’19 is equal to number of applicants who attempted SAT’19, then what can be the possible ratio of applicants who attempted SAT’19 to those who attempted SAT’20?
(a) 1 : 1
(b) 4 : 5
(c) 21 : 20
(d) 3 : 4
(e) 7 : 8
Q5. How many applicants filled CAT’20?
I. no. of applicants who attempted CAT’18 is same as no. of applicants who filled MAT’19.
II. no. of applicants who did not attempt CAT in all given years together is equal to no. of applicants who did not attempt MAT in all given years together.
(a) Both statements together are necessary
(b) Either statement I alone or II alone is sufficient
(c) Only statement I alone is sufficient
(d) Both statements together are not sufficient
(e) Only statement II alone is sufficient
Solutions
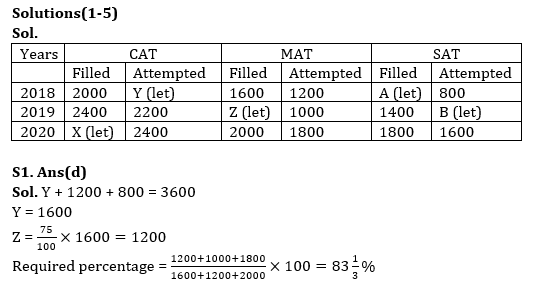


.





 Quantitative Aptitude Quiz For Bank Main...
Quantitative Aptitude Quiz For Bank Main...
 Quantitative Aptitude Quiz For Bank Foun...
Quantitative Aptitude Quiz For Bank Foun...





