Quadratic Equation Questions For Bank Exams

Quadratic equation questions are one of the most frequently asked topics in bank examinations such as IBPS PO, SBI PO, IBPS Clerk, RBI Assistant, and other competitive banking exams. These questions are considered highly scoring because they mainly test calculation speed, accuracy, and basic algebraic concepts. Candidates who practice this topic regularly can solve questions within a few seconds and secure good marks in the quantitative aptitude section.

Quadratic Equation Questions For Bank Exams

In bank exams, quadratic equation questions are generally asked in comparison-based formats where candidates need to compare the roots of two equations and determine the correct relationship between them. To solve such questions quickly, aspirants must have a strong understanding of factorization, simplification, square values, and root properties. Since these questions consume less time compared to lengthy arithmetic problems, they also help candidates improve overall time management during the exam.

What is a Quadratic Equation?

A quadratic equation is a polynomial equation of degree two, typically represented as ax² + bx + c = 0 where a, b, and c are real numbers, and a ≠ 0. The solutions to quadratic equations are known as roots or zeroes (two distinct real roots, one real root, or complex roots, depending on the values of a, b, and c.)

Types of Quadratic Equations

1. Factorizable Quadratic Equations: These equations can be factored into linear factors. For example, (x – 2)(x + 3) = 0.
2. Roots of Quadratic Equations: The roots of a quadratic equation can be found using the quadratic formula: x = [-b ± √(b² – 4ac)] / (2a).
3. Nature of Roots: Based on the discriminant (b² – 4ac), quadratic equations can have real and distinct roots, real and equal roots, or complex roots.

How to Solve Quadratic Equations

1. Factorizable Quadratic Equations: Factorizing quadratic equations is one of the simplest methods, especially when the equation is factorizable.
   • Identify common factors and attempt to factorize the quadratic expression.
   • Example: 𝑥² − 5𝑥 + 6 = 0 can be factored as (𝑥−2) (𝑥−3)=0.
   • Solve each factor individually to find the roots, i.e. 𝑥 = 2, 3.
2. Quadratic Equations Requiring the Quadratic Formula:
   • Use the quadratic formula: 
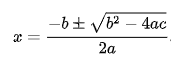
   • Substitute the values of 𝑎, 𝑏, and 𝑐 from the given quadratic equation.
   • Compute the discriminant (𝑏²−4𝑎𝑐) to determine the nature of roots.
   • Example: 2𝑥² + 5𝑥 − 3 =0.
     • Here, 𝑎=2, 𝑏=5, and 𝑐=−3
     • Substitute these values into the quadratic formula and solve for 𝑥.
   • So 𝑥= 1/2, −3.
3. Word Problems Involving Quadratic Equations:
   • Translate the given problem into a quadratic equation.
   • Example: “The product of two consecutive integers is 42. Find the integers.”
     • Let 𝑥 represent the smaller integer. The next consecutive integer is 𝑥+1.
     • Form the equation: 𝑥(𝑥+1)=42.
     • Solve the quadratic equation to find the integers.
   • So, 𝑥 = 6; 𝑥+1=7

Practice Questions for Bank Questions

Directions (1-5): In each of these questions, two equations (I) and (II) are given. You have to solve both equations and give the answer
(a) If x>y
(b) If x≥y
(c) If x<y
(d) If x≤y
(e) If x = y or no relation can be established between x and y

Q1. I. x² + 13x – 114 = 0
II. y³ = 216

Q2. I. x² − 6𝑥 + 12 = 4
II. y² + 4𝑦 − 10 = −13

Q3. I. 12x² − 7𝑥 + 1 = 0
II. 20y²− 9𝑦 + 1 = 0

Q4. I. x² + 26𝑥 + 165 = 0
II. y²+ 23𝑦 + 132 = 0

Q5. I. x²  + 𝑥 − 6 = 0
II. 15y²− 11𝑦 + 2 = 0

Direction (6 – 10): In each of the following questions two equations are given. Solve these equations and give the answer:
(a) if 𝑥 ≥ 𝑦, i.e., 𝑥 is greater than or equal to 𝑦
(b) if 𝑥 > 𝑦, i.e., 𝑥 is greater than 𝑦
(c) if 𝑥 ≤ 𝑦, i.e., 𝑥 is less than or equal to 𝑦
(d) if 𝑥 < 𝑦, i.e., 𝑥 is less than 𝑦
(e) 𝑥 = 𝑦 or no relation can be established between 𝑥 and 𝑦

Q6. (i) x² + 9 = 73
(ii) y² = 512

Q7. (i) x² + 11x + 18 = 0
(ii) y² + 19y + 90 = 0

Q8. (i). x²  − 10𝑥 + 21 = 0
(ii). y² – 5𝑦 + 6 = 0

Q9. (i) 2x² + x − 1 = 0
(ii) 2y² + 3y + 1 =0

Q10. (i). 2x² + 13x + 21 = 0
(ii). 2y² + 11y + 14 = 0

Direction (11 – 15): In each of these questions, two equations (I) and (II) are given. You have to solve both the equations and give the answer.
(a) If x=y or no relation can be established.
(b) If x>y
(c) If x<y
(d) If x≥y
(e) If x≤y

Q11. (I) x³ – 12 – 1319 = 0
(II) y² – 21 – 100 = 0

Q12. I. 12x²  − 7𝑥 + 1 = 0
II. y² + 23𝑦 + 132 = 0

Q13. (I) x² + 9x – 52 = 0
(II) 12y² + 16y + 4 = 0

Q14. (I) x² – x – 210 = 0
(II) y² – 31y + 240 = 0

Q15. (I) 2x² – 8x – 24 = 0
(II) 9y² – 12y + 4 = 0

Directions (16-20): In each question, two equations (I) and (II) are given. You should solve both equations and mark the appropriate answer.
(a) If x > y
(b) If x ≥ y
(c) If x < y
(d) If x ≤ y
(e) If = y or the relationship cannot be established.

Q16. I. 2x² – 7x + 5 = 0
II. y² – 3y + 2 = 0

Q17. I. x² – 25x + 156 = 0
II. y² – 29y + 210 = 0

Q18. I. x² + 20x + 96 = 0
II. y² + 15y + 56 = 0

Q19. I. x² – 3x – 40 = 0
II. 2y² + 11y + 15 = 0

Q20. I. x² – 16x + 64 = 0
II. y² – 14y + 48 = 0

Strategies for Solving Quadratic Equations in Bank Exams

• Understand the Equation Type: First identify whether the equation can be solved through factorization, simplification, or formulas to save time.
• Use Factorization First: Factorization is the quickest method and helps solve most bank exam quadratic questions easily.
• Apply the Right Method: If factorization is difficult, use the quadratic formula or completing the square method.
• Maintain Speed and Accuracy: Solve quickly but carefully, as small calculation mistakes can lead to wrong answers.
• Practice Comparison Questions: Regular practice of comparison-based quadratic equations improves speed and decision-making.
• Improve Calculation Skills: Learn squares, cubes, and algebraic identities to simplify calculations faster.
• Use Shortcut Techniques: Option elimination and root observation methods can help solve questions quickly.
• Solve Mock Tests Regularly: Previous year papers and mocks help understand question patterns and improve time management.
• Avoid Wasting Time: Skip lengthy questions initially and attempt easier ones first.
• Revise Important Concepts: Regular revision of formulas and root properties strengthens understanding and confidence.